Grassmann: Las leyes empíricas sobre la visión del color

Hermann Günther Grassmann publicó el famoso artículo Sobre la teoría de la mezcla de los colores (Über die Theorie der Farbenmischung) en 1853. Es históricamente interesante que en octubre de 1852 Grassmann hubiera anticipado su teoría sobre la mezcla de los colores en una conferencia dada en la Sociedad de Física de Stettin (Physikalischen Gesellschaft zu Stettin)—.

La ocasión para la elaboración de este artículo se la ofreció a Grassmann un artículo de Hermann von Helmholtz en el que este autor, dedicado a la investigación de los pares de colores cuyo resultado daba blanco —los colores complementarios—, afirmaba que sólo había podido encontrar el par de complementarios amarillo–índigo. Helmholtz avanzaba por ello la hipótesis de que para producir el blanco eran necesarios al menos tres colores espectrales.

En su artículo, Grassmann se proponía demostrar dentro de un marco teórico, que el modelo de Isaac Newton, por el contrario, implicaba la existencia de un número infinito de parejas de colores complementarios.

Los postulados de Grassmann

Para demostrar rigurosamente estas afirmaciones, Grassman formuló cuatro postulados, es decir: cuatro leyes que resumían la experiencia de un observador empeñado en el estudio de la mezcla aditiva de los colores. Estas leyes eran el fundamento teórico sobre el que se podía construir rigurosamente —matemáticamente— la teoría de los colores y expresar las propiedades del metamerismo en conexión con la síntesis aditiva.

Para fundamentar la teoría, Grassmann propuso considerar como términos básicos tres atributos perceptuales del color:

• Tono (Farbenton).
• Brillo del color (Intensität der Farbe).
• Brillo del blanco (Intensität des beigemischten Weiss), es decir, el brillo del componente acromático del color.

Grassmann introdujo también dos términos derivados:

• Brillo total = Brillo del color + brillo del blanco.
• Saturación = Brillo del color / brillo total.

Definidos estos términos, Grassmann avanzó los siguientes postulados.

1. Una sensación de color se especifica por completo con tres magnitudes: El tono, el brillo del color y el brillo del blanco.
2. Si una luz varía de forma continua, también la sensación del color de la mezcla aditiva con una otra luz que permanezca fija variarán de forma continua.
3. El resultado de una mezcla aditiva de colores depende sólo de su aspecto y no de su composición física.
4. La intensidad total de una mezcla aditiva de colores es la suma de la intensidad total de los colores mezclados.

Las leyes de Grassmann como se ha llamado a estos postulados eran, en intención del autor, afirmaciones evidentes que constituían la base a partir de la cual extraer por deducción las demás afirmaciones de la colorimetría.

La primera ley de Grassmann

Este postulado afirma que para definir una sensación de color es necesario y suficiente especificar tres magnitudes independientes. Newton ya había establecido que cualquier color —espectral o no— se podía especificar como la mezcla de una determinada cantidad de un color espectral con una determinada cantidad de blanco. Las tres magnitudes que especifican un color cualquiera son por tanto —para Newton y para Grassmann— el tono (Farbenton), es decir, el único color espectral que mezclado con blanco da el color en cuestión, el brillo del color (Intensität der Farbe) y el brillo del blanco (Intensität des beigemischten Weiss).

Grassmann describió también un dispositivo experimental con el que es posible medir estas tres magnitudes y presentó este primer postulado como algo experimentalmente evidente en tanto que…

Hasta ahora ningún observador ha permitido dar otro elemento que determine la sensación del color y el mismo lenguaje al describir una sensación de color sólo conoce estos tres elementos.

Los diversos tonos constituyen una serie circular que incluye todos los colores del espectro especificables por su refractividad —como hacía Newton— o por su longitud de onda —como podría hacer Grassmann, que sin embargo se remite a las líneas de Fraunhofer.

Sobre este punto, Grassmann comete un error que sin embargo no invalida su teoría. De hecho, juzgaba igual el tono del extremo rojo y del extremo púrpura del espectro, más o menos como hacía Newton, y llamaba "púrpura" a este tono, lo que le permitía cerrar el espectro de forma circular.

En realidad, como demostraría Helmholtz, los dos extremos (rojo y púrpura) no tienen el mismo matiz y ninguno de los dos es púrpura. Sin embargo, es cierto que mezclando aditivamente rojo y púrpura se obtienen diversos grados de púrpura. Este error hizo extraer a Grassman conclusiones erróneas a propósito de los colores complementarios.

En este primer postulado, Grassmann indica aquello que hoy día se denominan las dimensiones del espacio de los colores, introduciendo tres magnitudes independientes. La cuestión de las dimensiones y de su independencia se contenía en los fundamentos mismos de la obra principal de Grassmann, Ausdehnungslehre, donde Grassmann tuvo oportunidad de verificarla con ejemplo concreto de la naturaleza.

Grassmann afirmó, presentando una base específica, que las dimensiones del espacio de los colores son tres. La base está formada por el tono, la intensidad del color y la intensidad del blanco. Como se aclara más adelante, la base también puede estar formada por otra terna, por ejemplo, la cantidad de tres colores independientes —los míticos tres colores primarios perseguidos desde finales del setecientos—.

La segunda ley de Grassmann

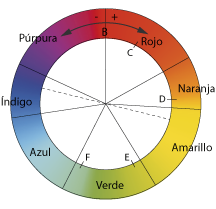
Para Grassmann, un tono varía de forma continua cuando varía de forma continua la longitud de onda y además, cuando llega a la máxima longitud de onda se pasa a la mínima (púrpura) y viceversa (a través del púrpura). El paso del púrpura al rojo a través del púrpura es continuo para el ojo, como es el caso de cualquier otra pareja de colores vecinos.

aunque las observaciones no han permitido establecer todavía los límites en los cuales las distintas longitudes de onda se corresponden con la misma sensación de color.

Una sensación de color varia de forma continua cuando varían de forma continua el brillo del color, el brillo del blanco y, si el brillo del color no es nulo, también el tono. Si el brillo del color es nulo —es decir, si las variaciones se producen a través del blanco—, un tono se puede transformar de forma continua en otra longitud de onda completamente distinta.

Según Grassmann

también este segundo postulado se confirma por la experiencia como un salto que hasta ahora nadie había percibido.

Sobre el tema de la continuidad, Grassmann se separa claramente de la descripción de Newton, quien por el contrario había privilegiado una división discreta del espectro en siete colores principales. Grassman, por el contrario, asumió esta condición de continuidad de modo tan riguroso que llega a suponer que el púrpura tiene el mismo aspecto que el rojo extremo, de modo tal que el círculo se cierra definitivamente. . Como ya se ha dicho, la formulación se vuelve correcta introduciendo una serie de colores entre el rojo y el púrpura , no sólo un color —el púrpura—, el púrpura, sino una serie de púrpuras. Con esta modificación, la experiencia confirma este postulado: No se han observado cambios bruscos del color al variar de forma continua la luz que produce la sensación.

La tercera ley de Grassmann

El tercer postulado tiene gran importancia porque permite abstraer las características físicas de la luz y hablar simplemente de colores. Eso ha permitido a Grassmann interpretar los colores como vectores y la mezcla de dos colores como la suma de dos vectores.

Ya se había visto en Newton que dos colores que parecen iguales pueden tener características espectrales distintas. Por ejemplo: El color M se puede formar mezclando A y B o mezclando C y D. En el primer caso, la característica espectral de M es la suma de las características espectrales de A y B, y en el segundo caso de C y D. Dos colores que se muestran iguales pero que tienen características espectrales distintas se llaman colores metaméricos.

Cabe preguntarse si dos colores metaméricos —es decir, dos colores visualmente iguales pero físicamente distintos— que se mezclan con un tercer color dan como resultado dos colores iguales o, por el contrario, el resultado de la mezcla depende también de las característica físicas. La experiencia que proporciona la experiencia es que el resultado de una mezcla de colores es independiente de sus características espectrales y depende sólo de su aspecto.

La cuarta ley

Es decir, la intensidad de una mezcla es aditiva. De hecho, este postulado se conoce también como la "aditividad de la luminosidad" y como ley de Abney. Hoy día se sabe que esta afirmación sólo es verdad en algunos casos y el mismo Grassmann apuntaba que

Esta ley no está tan bien fundamentada como las precedentes, pero por las observaciones teóricas parece la más probable.

Por sugerencia de Helmholtz, esta afirmación se usa para definir la luminancia, es decir, la magnitud fotométrica correspondiente a la magnitud radiométrica correspondiente de la radiancia.

Como resaltó MacAdam [7], el término intensidad, que es "apropiado sólo para fuentes puntiformes y no para amplias áreas de color como las que Grassmann discute".

Los colores complementarios

Aparte de enumerar los cuatro postulados, Grassmann no saca ninguna consecuencia. De los dos primeros postulados se puede deducir matemáticamente que "para cada color existe otro color espectral que, mezclado con el primero, da blanco" o, en términos modernos, que para cualquier color existe un color espectral aditivamente complementario.

Por todo lo dicho más arriba, esta conclusión no es correcta. Las distintas gradaciones de verde no tienen complementarios espectrales. Los complementarios del verde son precisamente aquellos púrpuras —mezcla de púrpura y rojo, por tanto no espectrales— que Grassmann no llegaba a considerar en la serie de los tonos y que fueron introducidos por Helmholtz.

La representación geométrica de los colores

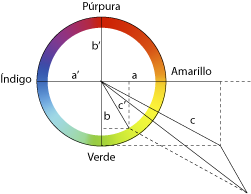
Establecida la cuestión de los colores complementarios, Grassmann introduce la representación geométrica (que hoy llamamos vectorial) de los colores. Los cuatro postulados garantizan que los colores obedecen a las leyes del baricentro y que su mezcla se pueden representar como sumas geométricas, aquello que Grassmann ya había representado en la Ausdehnungslehre (publicada en 1844) y en la que había demostrado que el baricentro de dos pesos A y B aplicado en los puntos a y b se puede calcular mediante una regla descrita hoy en cualquier manual de física general.

Se colige que cada color se puede representar en sus tres dimensiones con un punto y un peso en el círculo cromático. La dirección en la que este punto C sale del centro indica el tono, el peso del punto, la intensidad total de la luz. El producto de la intensidad total para la distancia del centro es la intensidad del color. El producto de la intensidad a la periferia es la intensidad del blanco. Si se define la saturación como la intensidad del color dividido por la intensidad de la luz, esa saturación se representa simplemente como la distancia del centro.

La conclusión de Grassmann es que de sus cuatro leyes, cada una ampliamente confirmada por la experiencia, se deducen resultados que están de acuerdo con la norma empírica de Newton y que esa deducción se hace "de forma puramente matemática".

Sin embargo, según Grassmann, el modo en el que Newton distribuye los colores homogéneos sobre la circunferencia de su círculo necesita una revisión total. Esta revisión sería realizada por Helmholtz y sus discípulos y llevaría en 1931 a la definición del diagrama de cromaticidad tal y como lo conocemos en la actualidad.

Las versiones modernas de las leyes de Grassmann

Los primeros reflejos de las leyes de Grassmann se encuentran en Helmholtz y Maxwell. Helmholtz la emplea y da una versión propia en su Manual de óptica fisiológica [13], mientras que Maxwell lo usa para comenzar a medir la ubicación de los colores espectrales, un objetivo indicado por el mismo Grassmann en su artículo. König y Dieterici perfeccionaron sucesivamente el trabajo de Maxwell y su determinación de los colores espectrales es el punto de partida de todas las investigaciones en este campo [9].

Desde entonces se encuentran en la literatura distintas formulaciones de las leyes de Grassmann [9], entre ellas las de Erwin Schrödinger, Manfred Richter o P. J. Bouma. Krantz [12] da una exposición matemática formal. Indicando con el símbolo de igualdad = la correspondencia metamérica entre estímulos de color, con el singo matemático de suma + la mezcla aditiva de estímulos de color y dados los estímulos de color A, B, C y D, se exponen las siguientes propiedades:

Simetría

Si A = B entonces B = A

Transitividad

Si A = B y B = C entonces A = C

Proporcionalidad

Si A = B entonces a × A = b × B para todo número real a ≠ 0.

Aditividad

Si A = B y C = D entonces (A + C) = (B + D). Si A = B y A + C = B + D entonces C = D.

Las primeras dos propiedades (juntas en la propiedad reflexiva A = A) definen una relación de equivalencia entre los estímulos de color, la relación entre los estímulos metaméricos. Los colores pueden ser, por tanto definidos como clases de equivalencias entre los estímulos de colores que parecen corresponderse subjetivamente.

La tercera (proporcionalidad) establece la compatibilidad entre las variaciones de intensidad de un estímulo de color y la relación de metamerismo, afirmando pues que el metamerismo se conserva si hay una variación de intensidad.

De forma análoga, la cuarta propiedad (aditividad que se deriva de la tercera ley de Grassmann) afirma que la relación del metamerismo se conserva cuando a cada uno de los dos estímulos metaméricos se le mezclan estímulos metaméricos.

El conjunto de los estímulos de color constituyen por tanto (un cono convexo en) un espacio vectorial de números reales, que es el espacio del triestímulo. La primera ley de Grassmann afirma que este espacio es vectorial y tridimensional.

La validez de las leyes de Grassmann está actualmente en debate y hay que destacar que las leyes no son completamente ciertas para la visión humana en todas las situaciones [14].